DPO - Direct Preference Optimization
Direct Preference Optimization: Your Language Model is Secretly a Reward Model
Tutorial https://www.youtube.com/watch?v=hvGa5Mba4c8
Paper: https://arxiv.org/abs/2305.18290
Highlight
It solve the RLHF problem which aims to align the output of LLMs to the uer desires, for example, to give human-prefered outputs that are more polite, friendly, no descrimination, etc. but without using reinforcement learning, but the common SGD.
How?
Recall in RLHF, we train a reward model (e.g., Bradley Terry model) $r^*$ such that for a human-prefered answer $y_1$ and a unprefered answer $y_2$ for a given prompt $x$, the probability that $y_1$ ranks before $y_2$
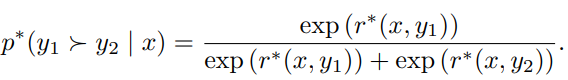
has a high value.
We can collect a dataset
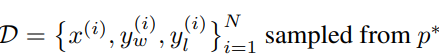
where $y_w$ and $y_l$ are winning and losing answers respectively, to tain this reward model $r_\phi(x, y)$, with the loss:
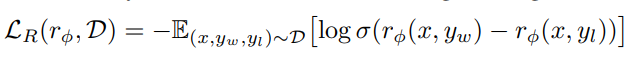
Once we get the reward model, we use it to fine-tune our LLM $\pi_\theta(y|x)$:
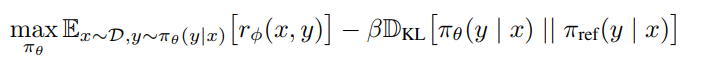
The first term in the square bracket is to ensure that the generate answer $y$ by $\pi_\phi$ has high reward value, and the second term is a regularization to make sure that the fine-tuned model doesn’t deviate the original LLM, or the reference model, too much. Otherwise, the model will simply generate answers that are polite, friendly, etc, but without actually answering x.
The above optimizaiton is not differentiable as the term under the expectation symbol is not fixed, it is actually a distribution depending on $\pi_\phi$. So we cannot use SGD to train it, since the sampling process under the expectation is not differentiable, like we saw in VAE.
My note:
In VAE, the authors use a reparameterization trick, which is feasible because they suppose the distribution under expectation is a Gaussian noise. However, the distribution of $y\sim\pi_\phi(y|x)$ is not Gaussian, so we cannot use the same strategy.
To solve that, RLHF uses reinforcement learning. However, the authors of DPO find the analytical solution of the above optimization problem, given the reward model $r$:
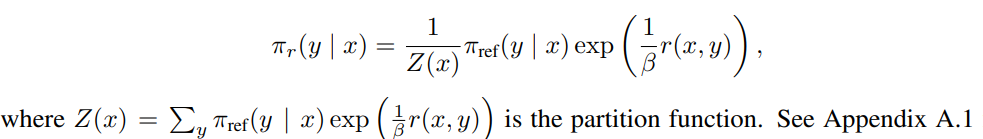
It is not easy to compute because of the Z.
How the magic happens?
So, from the above equation, we get also get an expression of the reward model r:
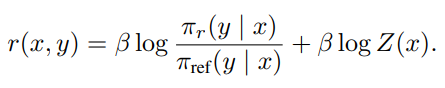
which is expressed by the reference model and the fine-tuned model. We can then substitute this formulation to the loss function of training the reward model, and we get
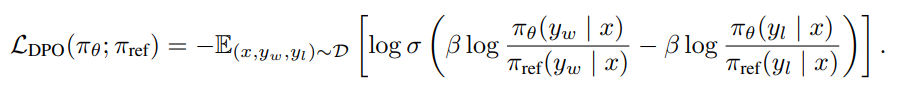
This step actually cancels Z out, and we are directly fine-tuning our LLM model, and jump the step of training a reward model!
This can achieve exactly the same goal as we want to achieve in the first place, the regularization, or the KL divergence between the fine-tuned model and the reference model is implicitely included in the DPO training objectives.