Megatron-LM (2)
Efficient Large-Scale Language Model Training on GPU Clusters Using Megatron-LM
paper (2021 arxiv): https://arxiv.org/abs/2104.04473
Contributions
Based on Megatron-LM, the authors further adopt pipeline model parallelism via the proposed interleaved 1F1B pipeline schedules to scale the LLM training to thousands of GPUs, because of the dramatic increase in model sizes.
Methods
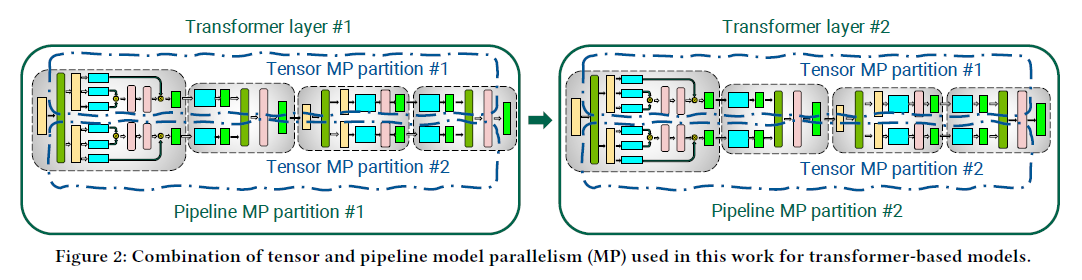
Basically, it combines tensor parallelism (proposed in Megatron-LM) and pipeline parallelism for model parallelism. Assume tensor-parallel size is $t$, pipeline-parallel size is $p$ (also said as the number of pipeline stages), and data-parallel size is $d$, then the total number of GPUs is $ptd$.
First, let's get familiar with some concepts:
GPipe pipeline schedule
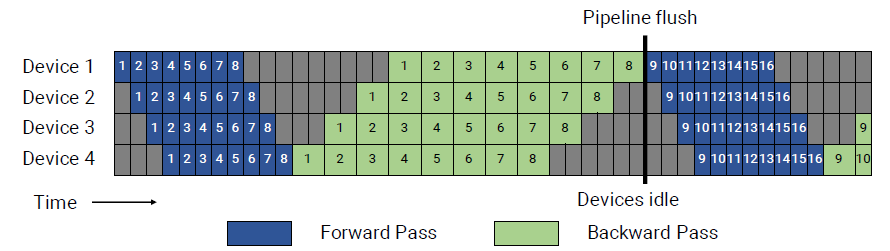
The grey area represents pipeline bubble where devices are idle. Pipeline flush, I guess, is the end point of the backward pass at each iteration.
Here, the number of microbatches in batch is $m$, and assume the time to execute a single microbatch’s forward and backward pass as $t_f$ and $t_b$. Then the total amount of time spent in the pipeline bubble is $t_{pb} = (p-1)\cdot (t_f + t_b)$, and the ideal processing time for the batch is $t_{id} = m\cdot (t_f + t_b)$. Therefore, the fraction of ideal computation time spent in the pipeline bubble (or called the bubble time fraction) is:
$$
\frac{t_{pb}}{t_{id}} = \frac{p - 1}{m}.
$$
The bubble time fraction should be as small as possible. The naive solution is to make $m \gg p$, however, this needs each device to store all the m microbatches’ activations for the gradient calculation in the backward pass, having a high memory footprint. In other words, the number of in-flight microbatches equal to the total number of microbatches $m$, so we have:
PipeDream-Flush schedule (upper part of the following figure)
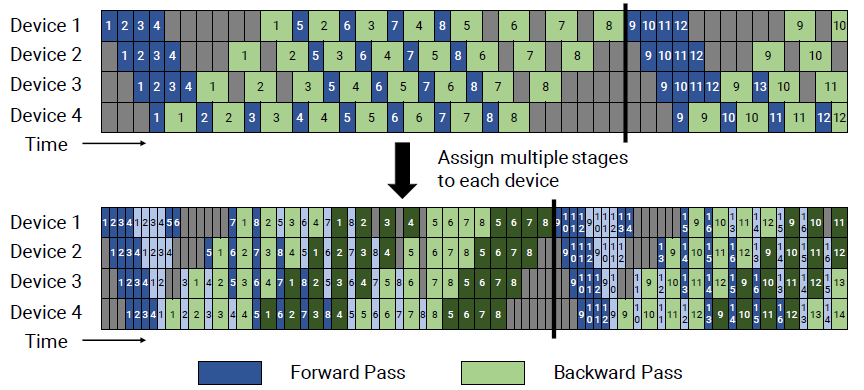
In this schedule, there is a warmup phase for each device for the forward pass. After the warmup, the device goes with a one forward pass followed by one backward pass, which is the so-called 1F1B schedule. In this way, the number of in-flight microbatches reduces to $p$ in maximum, while the bubble fraction time is the same. Therefore, PipeDream-Flush can be much more memory-efficient when $p \ll m$.
To reduce the bubble fraction time and keep the schedule memory efficient, the authors propose:
Interleaved 1F1B pipeline schedule (lower part of the above figure)
Briefly, each device can perform computation for multiple subsets of layers (or a model chunk), for example, device 1 has layers 1, 2, 9, 10, device 2 has layers 3, 4, 11, 12, and so on. Then just like the 1F1B schedule, they do an interleaved 1F1B schedule.
- Property 1: this needs the number of microbatches $m$ to be an integer multiple of $p$;
- Property 2: this reduce the pipeline bubble time to $(p-1)\cdot(t_f+t_b)/v$ where $v$ is the number of model chunks in each stage. Then the bubble time fraction reduces to $(p-1)/(m\cdot v)$.
- Property 3 (drawback): this introduces extra communication with the increase of $v$.
Higher-level experimental and analytical conclusion
The actual throughput for each device is affected by all the hyperparameters $p, t, d, B, b$ etc., where $B$ is the global batch size and $b$ is the microbatch size due to the communication overhead between devices. There are three takeaways
-
When using $g$-GPU servers, the tensor model parallelism should generally be set up to $g$. Based on that, pipeline model parallelism can be used across servers.
-
When combine data and model parallelism, for model parallelism, a total number of $t\cdot p$ GPUs should be used to fit the model memory, then data parallelism is used to scale up training.
-
The optimal $b$ depends on the characteristics and throughput of the model, $p$, $d$ and $B$.
Communication optimization
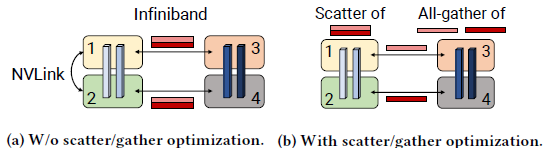
Simply, shown in the above figure, assume we have $t=2$, when send and receive between two consecutive pipeline stage (i.e., two servers according to conclusion 1), the naive way is to send the tensor on each GPU on the previous pipeline stage (server) to the second stage, where each pair of GPUs on the sender and receiver communicate with the exact same set of tensor. Instead, we can first divide (scatter) the tensor to be sent into $t$ parts equally and each GPU on the sender server send its part to the GPU on the receiver server, then use all-gather operator to gather the tensor. We call this scatter/gather optimization that reduce the communication to $1/t$.
General accelerator-agnostic ideas
- Smartly partitioning the model training graph to minimize the amount of communication while still keeping device active (they are saying the interleaved 1F1B pipeline schedule).
- Minimizing the number of memory bound kernels with operator fusion and careful data layout (they might be saying the fusion of output embedding with the cross entropy loss function to reduce the communication overhead).
- Other domain-specific optimizations (like the scatter-gather optimization).
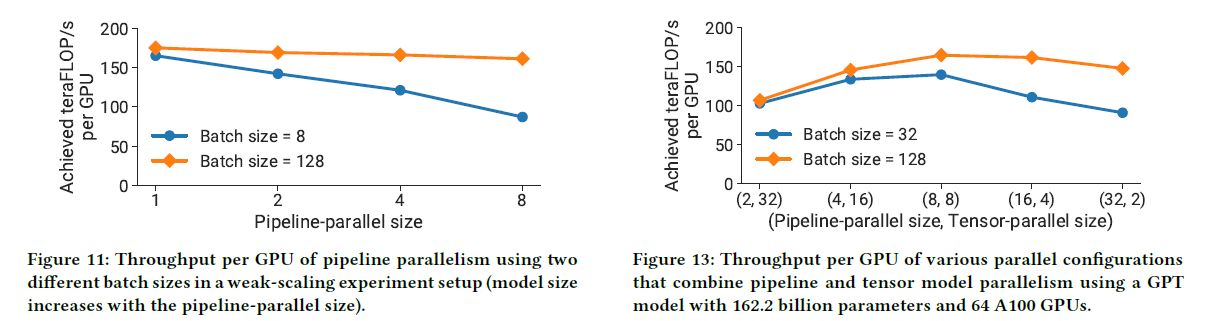
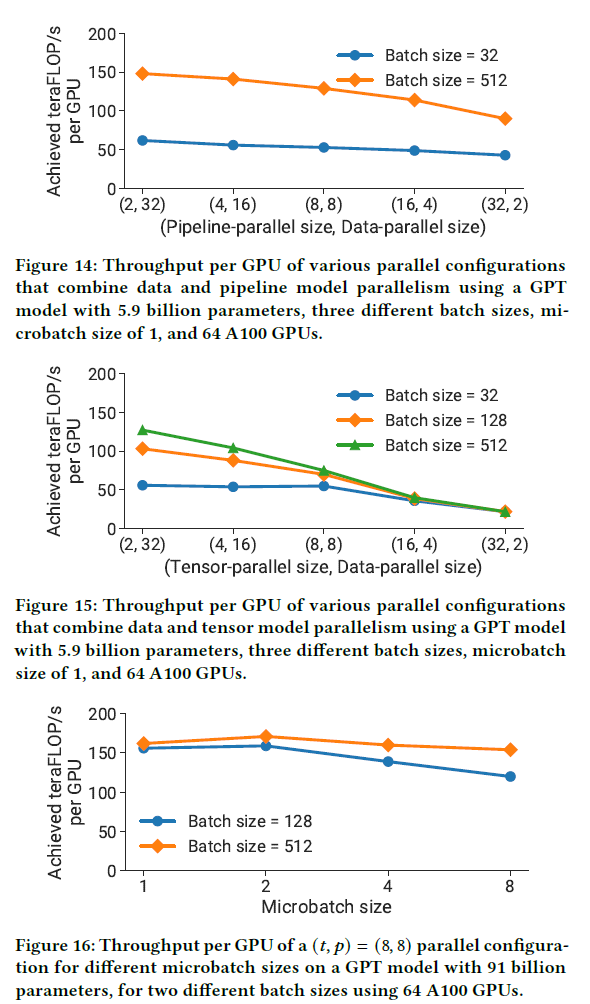
Experiment results