Megatron-LM (3)
Reducing Activation Recomputation in Large Transformer Models
paper (2022 arxiv): https://arxiv.org/abs/2205.05198
Contributions
Briefly, the authors based on tensor and pipeline model parallelism, find that the previous parallelism cannot reduce the memory needed for activations while maintaining high device utilization. They propose sequence parallelism and selective activation recomputation.
Methods
Sequence parallelism
Let’s first analyze the activation memory during training for a single transformer layer without gradient checkpointing (or activation recomputation).
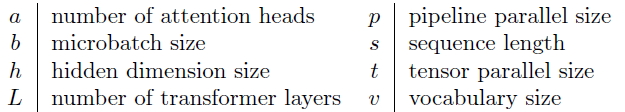
Above is the transformer structure with layer normalizations rearranged in Megatron-LM. Supposing the network and activations are stored in a 16-bit floating point format (2 bytes for each element) and the dropout masks only need 1 byte to store. The activation memory (in bytes) needed for each component is
- LayerNorm: $4sbh$
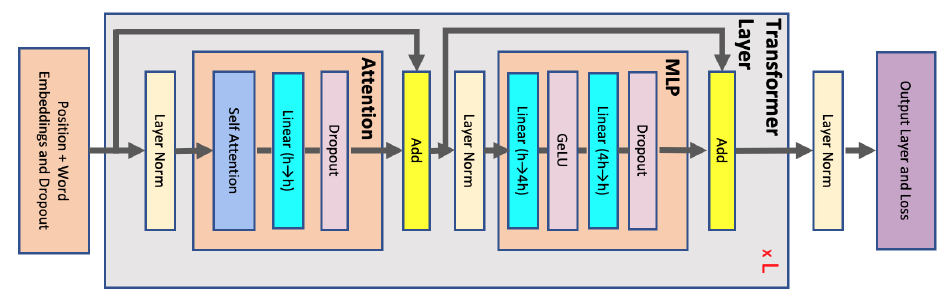
- Self Attention as follows:
Q, K, V: $6sbh$
QK^T + Softmax output: $2s^2b$
Dropout mask: $s^2b$
Dropout output: $2s^2b$
Attention with V: $2sbh$
In total: $8sbh + 5s^2b$ - Linear ($h\rightarrow h, h\rightarrow 4h, 4h\rightarrow h$): $2sbh + 8sbh + 2sbh = 12sbh$
- Dropout (masks + output): $1sbh + 2sbh + 1sbh + 2sbh = 6sbh$
- GeLU: $8sbh$
In total: $34sbh + 5s^2b = sbh(34 + 5\frac{as}{h})$.
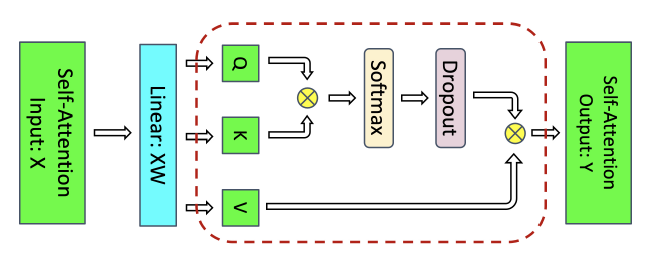
However, when applying tensor parallelism (above figure), the output of LayerNorm ($4sbh$), output of dropout layers and dropout masks ($4sbh + 2sbh=6sbh$) are stored in all GPUs. Therefore, $10sbh$ are not parallelized. Therefore, the activations memory per layer is:
$$sbh(10+\frac{24}{t}+5\frac{as}{ht})$$
The authors then propose sequence parallelism to also parallelize these $10sbh$ tensors along their sequency dimension:
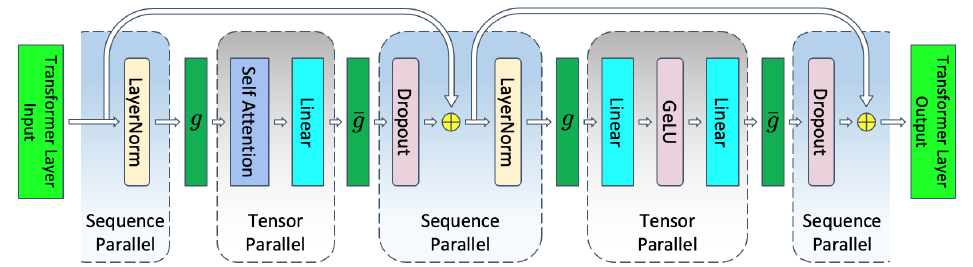
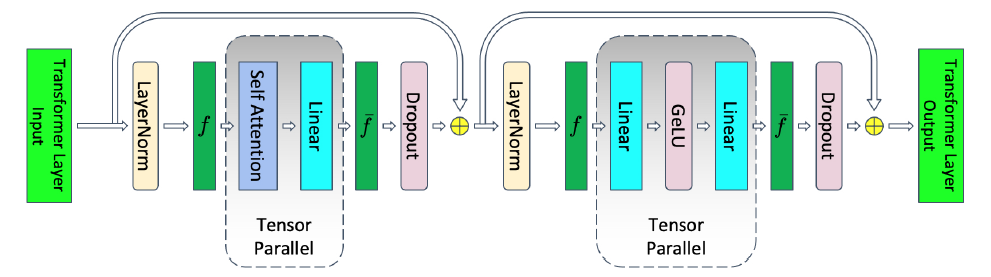
To do that, for example, apply sequence parallelism on the two side of MLP tensor parallelism, the method is illustrated as follows:
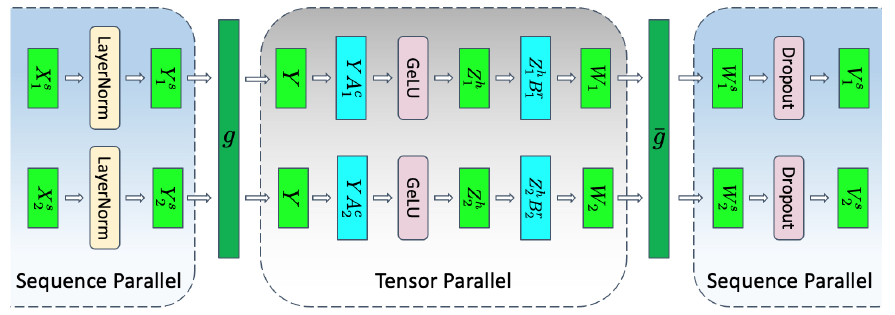
Particularly, before the “$g$” function, $Y_1^s, Y_2^s$ are the outputs from the previous sequence parallel stage which are divided along the sequence dimension, therefore, $g$ function uses “all-gather” operator to concatenate them and distribute the result to each tensor parallel device. The outputs of the tensor parallel stage should be processed with “all-reduce” that adds together the outputs and then distributed to each device for the dropout, instead, $\bar g$ uses “reduce-scatter” to scatter (or divide) the reduced results into different segments along the sequence dimension again, each sequence parallel GPU takes one segment for the dropout, followed by another tensor parallel stage.
In this way, all the activations are paralleled. There is no extra communications. Before sequence parallelism, for one forward and backward pass, it needs 4 all-reduce operations. Now, it needs 4 all-gather and 4 reduce-scatter operations, which have the same communication overhead.
Other notes
The authors also discussed the activations on input and output embeddings, which are negligible compared with the transformer layers.
Selective Activation Recomputation
Generally, we don’t store the softmax output, dropout mask and dropout output which take large amount of memory (the $5\frac{as}{ht}$ term). When doing backward pass, we recompute them based on the stored Q, K, V. However, the calculation of these activations is compute-efficient, so it makes more sense to recompute them.
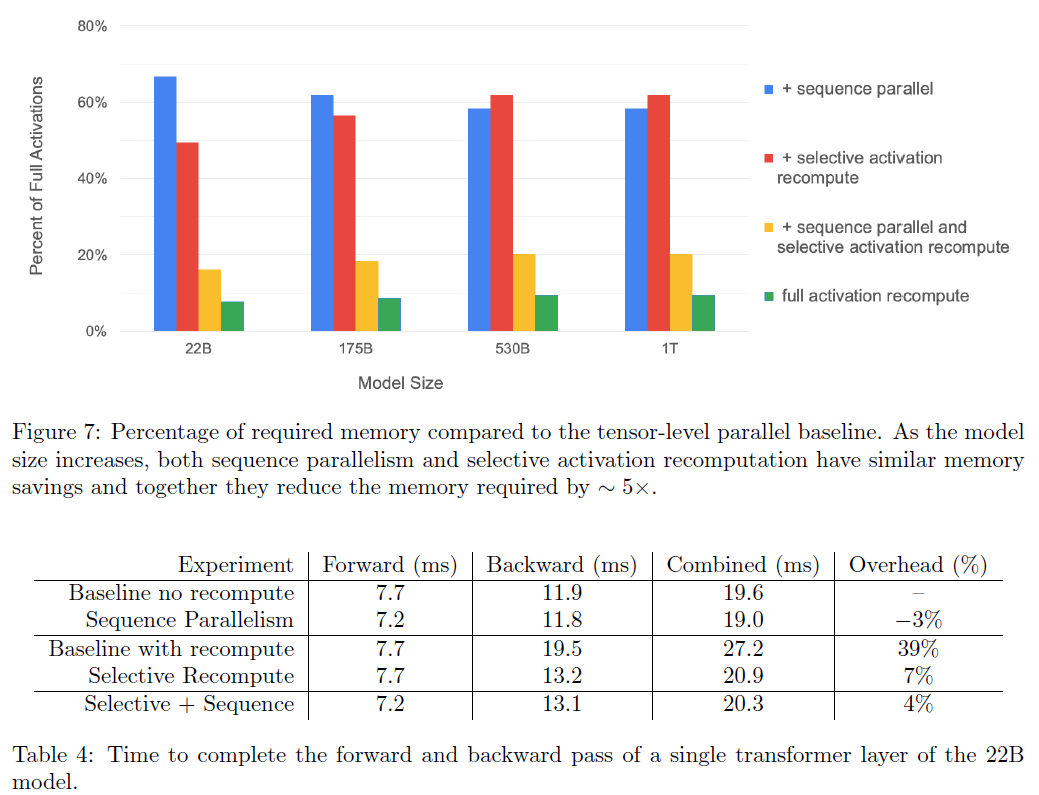
In Table 4, the observation is that the introduction of selective activation recomputation only slightly affects the training speed, while the introduction of sequence parallelism reduce the overhead and speedup training. When two techniques combined, the speed and overhead just slightly affected, but the activation memory per device is significantly reduced (all tensors to $1/t$), which is important for scaling to large models.