ZeRO-Infinity
ZeRO-Infinity: Breaking the GPU Memory Wall for Extreme Scale Deep Learning
paper (2021 arxiv): https://arxiv.org/abs/2104.07857
The highlight of the method
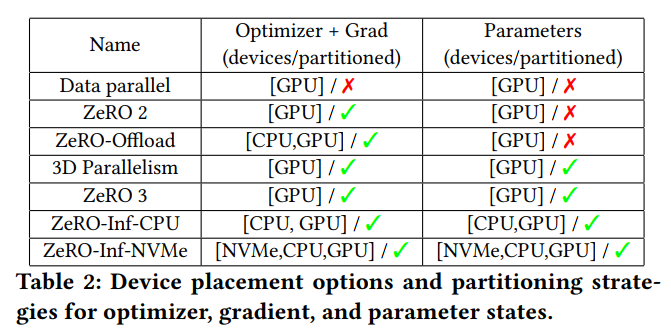
- The much larger models training can scale to with the same number of GPUs compared with prior methods.
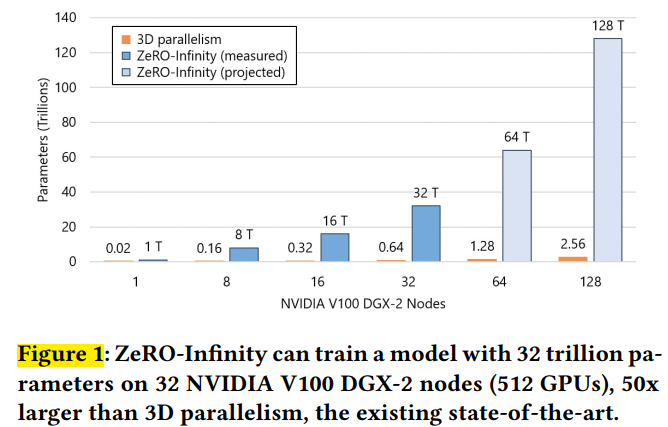
- High throughput and good scalability
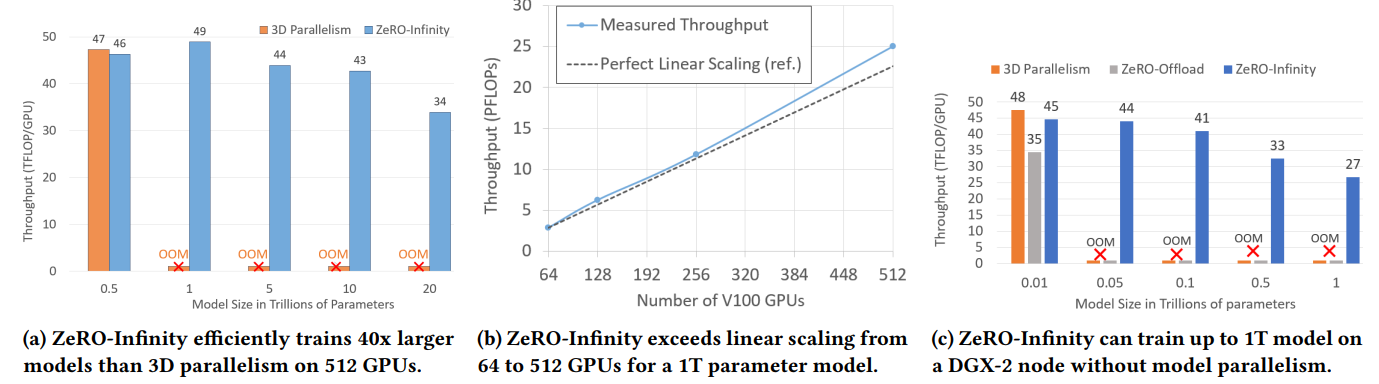
Surprisingly, even with small model size, ZeRO-Infinity performs comparably with 3D parallelism and ZeRO-Offload.
My memory on ZeRO-Infinity
Memory we have
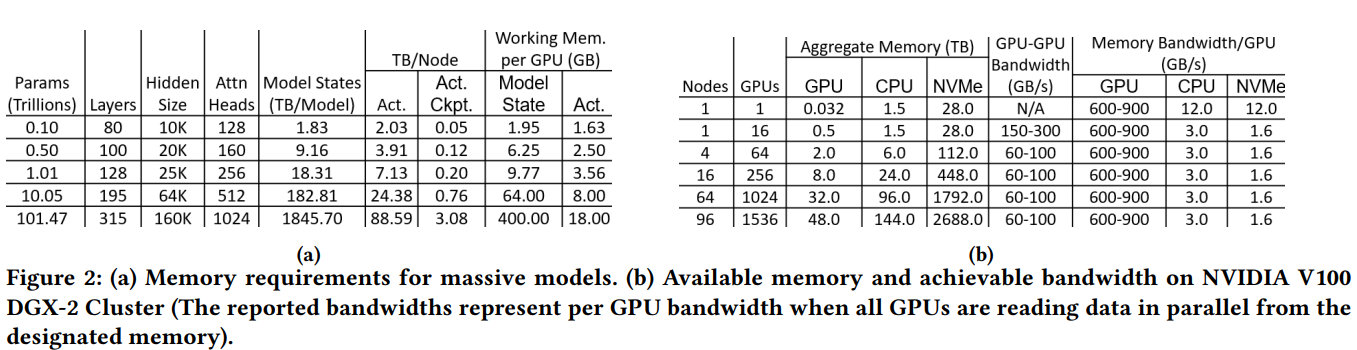
The above figure shows the memory requirement for different sizes of models, where sequence length is 1024 and batch size is 32 (most likely, as implied in the paper), and the memory bandwidth for communication between different devices (refer to the paper for detailed calculation).
Theoretically, for a single GDX-2 node with 16 GPUs, the aggregate memory on NVMe is 28T, allowing a 1-T model to be trained which requires about 19T memory during training (if activation checkpoints are used).
Requirement on memory bandwidth for efficient training
The problem is the bandwidth from GPU to CPU/NVMe is slow that would likely to be the bottleneck of throughput. How to fully use the slow memory bandwidth to prevent it being the bottleneck is the core of this paper.
By analyzing the equation of efficiency:

The $ait$ (arithmetic intensity) can be obtained for the following three parts: model parameters and gradients, optimizer states, and activation memory, respectively, by computing the total computation and data movement per training iteration for the transformer model. The $ait$ is a function of batch size, hidden dimension, and sequence length. After that, we let the $peak_{tp}$ is 70TFlops/GPU based on v100, and we can draw the curves of efficiency w.r.t. batch size, hidden dimension, and bandwidth, assuming the sequence length is 1024 (I am not going to details about how the $ait$ is calculated, please refer to the original paper):
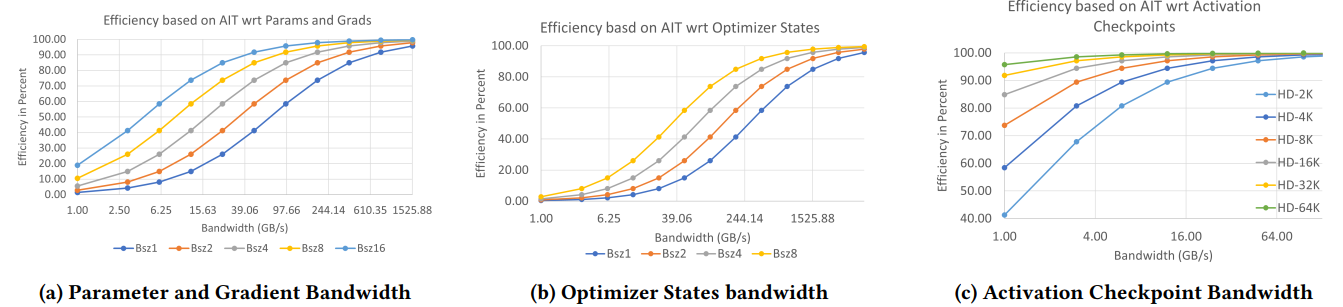
From the above figure, we got three important numbers for the bandwidth that can allow efficient training.
- For parameters and gradients, the bandwidth requirement is 70GB/s corresponding to an efficiency of 50%, because for this case, communication can be overlapped with computation, since forward and backward propagation are both executed sequentially. For example, while doing forward propagation for the $i$th operator, the parameters for $(i+1)$th operator can be moved at the same time (i.e., when applying ZeRO-3, move of parameters is actually broadcasting parameters from the host GPU of the parameters to other GPUs). The same mechanism applies to gradients and parameters during backward propagation.
- For optimizer states, the authors of the paper state that the communication cannot be overlapped with computation. Therefore, a bandwidth of 1.5TB/s is required in order to achieve a 90% efficiency.
- For activation checkpoint memory, a bandwidth of 2GB/s is obtained to also achieve a 50% efficiency due to the the possibility of overlapped computation and communication.
Note: ZeRO-Infinity is applied based on ZeRO-3
How to fully use memory to scale to trillion-parameter models?
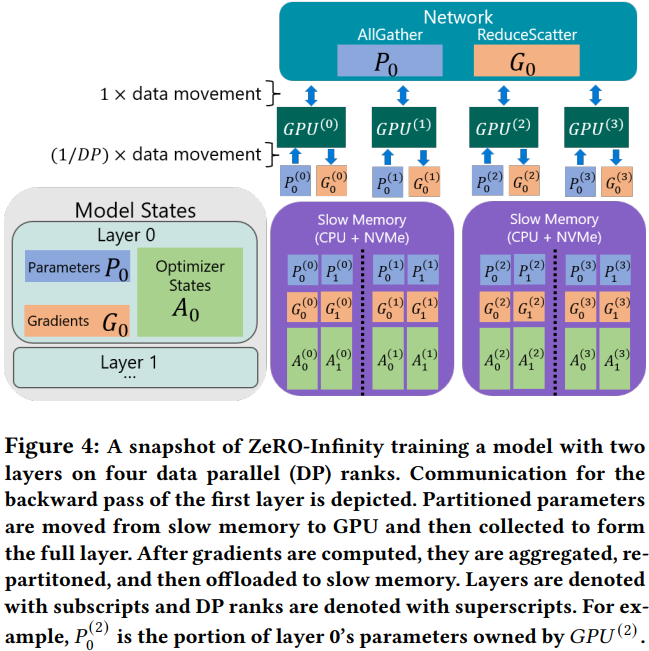
- Like above, just offload memory to CPU/NVMe (implemented with a proposed infinity offload engin by the authors).
- CPU offload for activation, as the memory requirement of activations are small.
- Reduce the working memory, by breaking down a large operator into small tiles that can be executed sequentially (the working memory for model state in Figure 2 (a) is calculated based on the largest operator, i.e., the h->4h linear projection. By using the tiling strategy, the linear operator is represented by a mathematically equivalent sequence of smaller linear operators).
How to fully use slow memory bandwidth to remain high training efficiency?
- For parameters and gradients
There are two strategies to enable efficient communication.- Now we are using ZeRO-3, in the original way, the parameters (usually of a individual operator) are broadcast from other GPUs whenever needed, during which the parameters located in the CPU or NVMe is first moved to the owner GPU via PCIe, followed by broadcast to other GPUs. This causes many idle PCIes because only the PCIe connected to the owner GPU is active. To solve that, the parameters of the individual operator is further partitioned into all the data parallel GPUs. In this way, the parameters of even an individual operator has many owner GPUs instead of only a single owner GPU. Therefore, during moving the data from CPU or NVMe to GPU, all the PCIes can be active, achieving an aggregate bandwidth linear to the data parallel degree. For example, with 1024 GPUs used in a data parallelism, the aggregate bandwidth for moving data from CPUs to GPUs can be 3TB/s (1024 * 3GB/s). The process is shown above, applying to both parameters and gradients.
- The second is called overlap centric design, which is also quite simple. Basically speaking, when doing the forward pass for the $i$th operator, the parameters of the $(i+1)$th parameters can be at the same time moved from CPUs to GPUs, and the parameters of the $(i+2)$th operator is moved from NVMe to CPUs. Same spirit is applied in backward propagation.
- For optimizer states
- A powerful C++ library called DeepNVMe for asynchronous communication that allows ZeRO-Infinity to overlap NVMe to CPU reads with CPU to NVMe writes, as well as the CPU computation for the optimizer step (bring the data from NVMe to CPU memory and back in chunks that can fit in the CPU memory to perform the optimizer step, one chunk at a time).
- Pinned memory management layer that reuses a pinned memory to gradually move the entire optimizer states memory from GPU to CPu or NVMe (pinned memory buffer is important to ensure high-performance tensor reads and writes).
Notes: the authors also propose “Ease inspired implementation” to ease use, please refer to the paper for details at section 7.