DeepSpeed-MoE
DeepSpeed-MoE: Advancing Mixture-of-Experts Inference and Training to Power Next-Generation AI Scale
paper (2022 arxiv): https://arxiv.org/abs/2201.05596
First, let’s look at how MoE architectures look like?
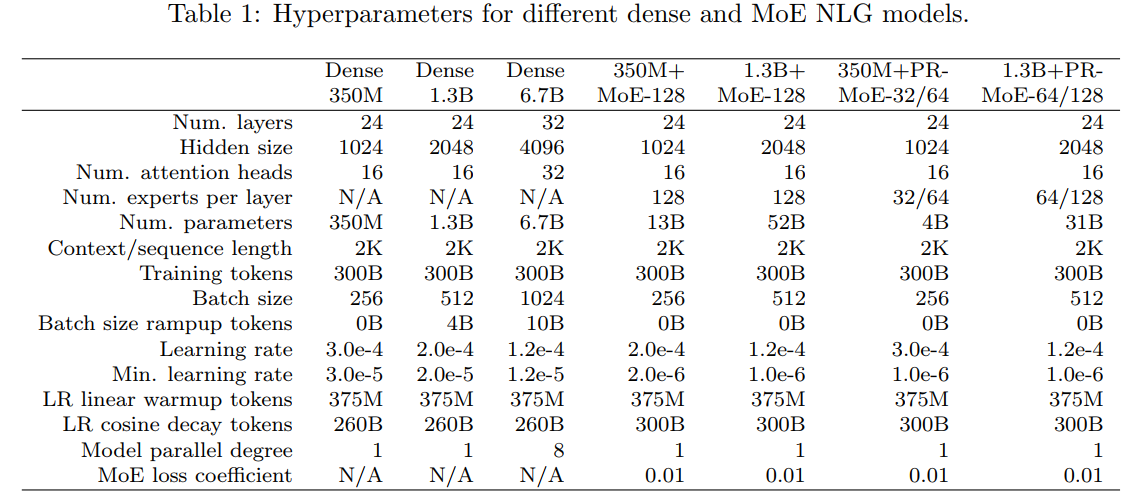
As shown above, basically, each MoE has a corresponding dense base model. For example, let the 350M dense model be the base model, then on every other feedforward layer, the feedforward layer is expanded with multiple branches (e.g., 128) where each feedforward branch can be seen as an expert on this layer, leading to a MoE architecture (e.g., 350M + MoE-128).
The number of parameters of MoE is tens times of bigger than the corresponding base model, but the training or inference cost is similar to the base model (assuming that the number of training tokens keeps the same), because only a single expert on each expert layer is activated for each token, via a gating function.
What other methods do we think about?
- Network pruning, especially channel pruning (we only activate a certain part of channels in each layer).
- Dynamic pruning, dynamic routing, where a gating function is used to make decisions about which channels, or which layers, will be activated.
What are we expecting?
- We expect that the quality of a MoE model should match the quality of a dense model that is much bigger than the MoE’s base model.
- Yeah, now maybe just point 1.
Second, lets’ train all the dense or MoE models.
First, how we train the big MoE model?
Simple, use data parallelism and expert parallelism. For data parallelism, ZeRO series are a good option. For expert parallelism, for each feedforward layer with experts, just partition the parameters along the expert dimension, for example, each GPU has an equal number of experts.
Since data parallel and expert parallel training are used, before feed the data to experts, we should use a all-to-all operator where we collect the tokens that should be
Do we get our expectations?
Regarding prediction performance
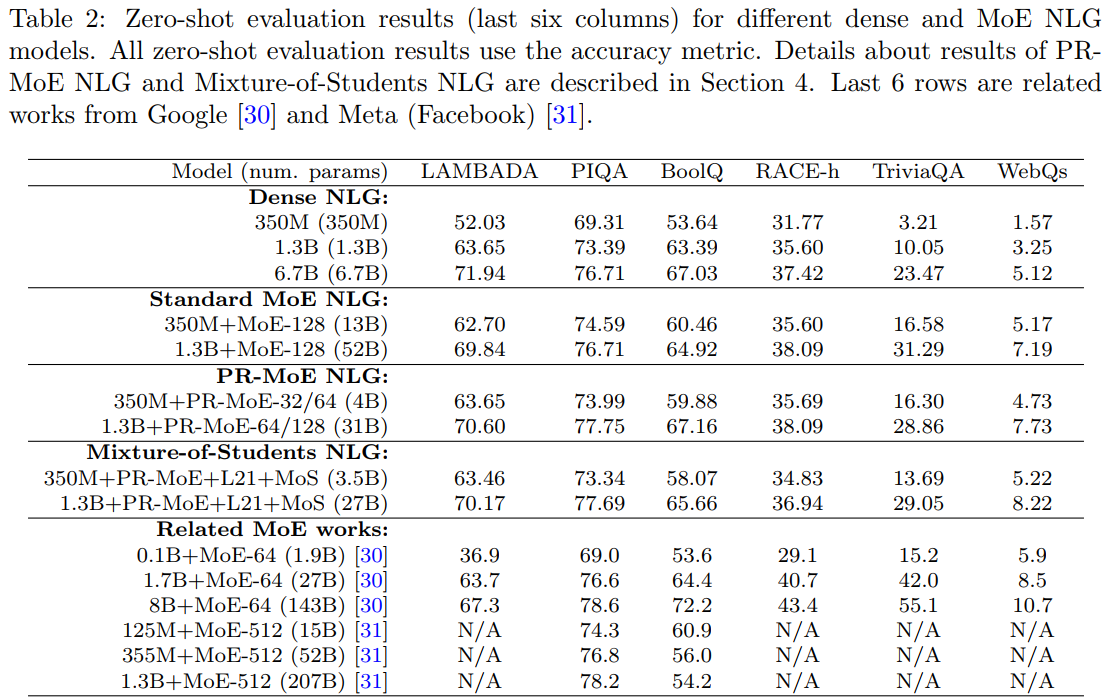
As shown above, the 350M+MoE-128 performs on par with the 1.3B dense model. Similarly, the 1.3B+MoE-128 performs on par with the 6.7B dense model.
Regarding training cost

1.3B+MoE-128 model achieves 5$\times$ efficiency compared with the 6.7B dense model.
What can we imagine?
We can train GPT-3 or MT-NLG 530B quality model with a 5$\times$ reduction in training cost, via MoE models, assuming that the scaling holds.
Third, PR-MoE and MoS
PR-MoE: Pyramid-Residual-MoE for smaller size and fast inference but same quality
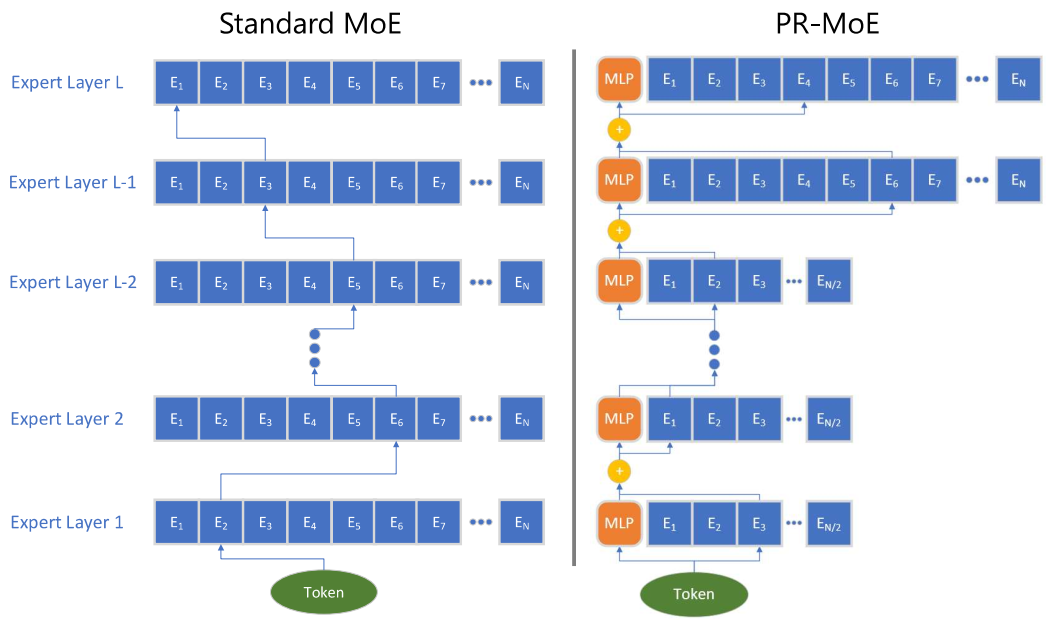
Here is the structure for PR-MoE. The first idea is that the deeper layers could be assigned with more experts while the shallower layers less, similar to the basic CNN structures.
The second idea is that we can fix one expert and dynamically select the second expert (as the residual) in the expert layers, in order to get the same quality as a Top-2 MoE.
But how to train PR-MoE in parallel?
Solution: flexible multi-expert and multi-data parallelism design that allows for training different parts of the model with different expert and data parallelism degree. For example, we have three parts in the architecture with 32, 64, and 128 experts respectively, and the number of GPUs available is 128. The design of parallelism degree could be:
| Non-expert parameters | Expert parameters in part with 32 experts | Expert parameters in part with 64 experts | Expert parameters in part with 128 experts | |
|---|---|---|---|---|
| Expert parallelism degree | N/A | 32 | 64 | 128 |
| Data parallelism degree (I guess using ZeRO) | 128 | 4 | 2 | 1 |
Note: The training process should be like this: for example, for the layers with 64 experts, each GPU has 1/128 part of the global batch as its minibatch for its non-expert parameters. For non-expert parameters, lets’ say the index of the expert in this GPU is i, the all-to-all operator will assign all tokens belonging to expert i based on the global batch, and the tokens will be partitioned into half and one half will be put to this GPU (because now the data parallelism degree is 2). It means the data fed to non-expert and expert parameters could be from different samples from different minibatches. During the backward propagation, the gradients are averaged following the index information of which data is fed to which parameter. Please also refer to Figure 7 below.
MoS: Mixture-of-Students: the student is now a MoE model too
The authors state that with standard KD where the student is a dense model, the distilled student model loses the sparse fine-tuning and inference benefits provided by MoE. So they make the student also a MoE model. To make the student smaller, they reduce the depth of each expert branch in the teacher model. The general KD loss is used that forces the MoS to imitate the outputs from the teacher MoE on the training dataset.
A strategy on training MoS
MoS is trained in two stages, where the first stage is the normal training with standard loss and KD loss. The second stage stops KD and only train with the standard loss. The motivation is that the student cannot perform as good as the teacher at the end of the training, and the authors hypothesize that the student don’t have enough capacity to minimize both losses, so it should focus on only one loss at the end.
Finally, DeepSpeed-MoE inference
It should be in the same spirit as in training PR-MoE. Here is the figure illustration:
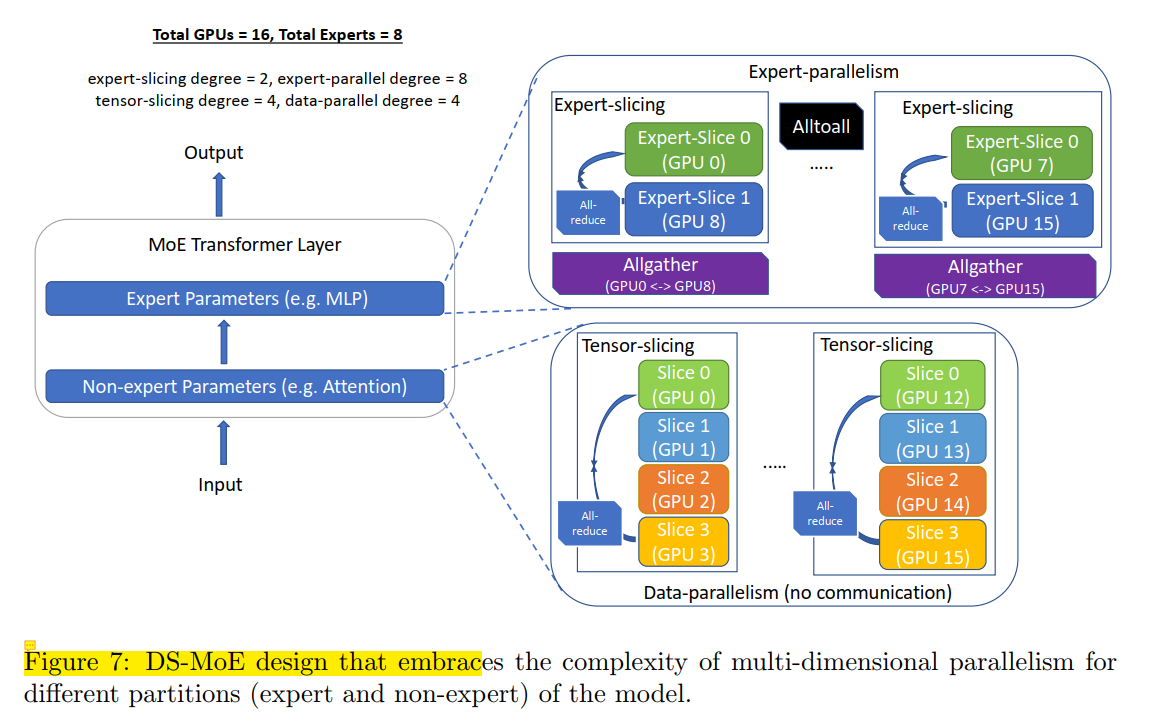
What I guess the process is:
in non-expert parameters, data parallelism and tensor-slicing model parallelism are used, the all-reduce is for model parallelism to average the output from different tensor slice before going to the next layer (just like Megatron-LM).
The next layer might be the router to calculate the probabilities for different experts for the following expert parameters. Then because we have used 4-degree data parallelism, but the parallelism for expert parameters doesn’t use it, so we need to use “allgather” to gather the outputs from different data parallelism groups, so that each expert parallelism group see all the data, and takes the corresponding tokens that it is allocated according to the router response for each token. In each expert parallelism group, it further applies expert-slicing to increase parallelism by vertical/horizontal partitioning of expert parameters, and use “all-reduce” to average the output. Among different expert parallelism groups, it uses “alltoall” to update the information.
The authors also designed some subsystems to optimize communications for the collective operators.