Flash Attention 1 & 2
FlashAttention: Fast and Memory-Efficient Exact Attention with IO-Awareness
paper (2022 arxiv): https://arxiv.org/abs/2205.14135
Background: compute-bound and memory-bound
- The performance on throughput of transformer layers can be either compute-bound or memory-bound. The higher the arithmetic intensity, the more likely to be compute-bound.
- Compute-bound operators include matrix multiplication where the computation takes more time than communication or data movement, memory-bound operators perform in an opposite way, including element-wise operators, and reduction, e.g., sum, softmax, batch norm, etc.
Equation of attention
Here I just take a snip from the paper:

Standard attention implementation is memory-bound
It is memory-bound due to the quadratic complexity of memory reads/writes (or data movement) to the sequence length, i.e., $O(N^2)$, due to the softmax function and other element-wise operations applied to the attention matrix like masking, dropout.
In addition, GPU has hierarchy memory structure that comprises multiple forms of memory of different sizes and speeds:

We could see that SRAM has much higher bandwidth than HBM (high bandwidth memory), but unfortunately, the standard implementation involves the $O(N^2)$ data movement from and to HBM, becoming a bottleneck of performance:

Note: from my personal view, seems like the statement of the issue is problematic since we could simply don’t write $S$ to HBM and continue using it to computer $P$. In line 3, we can also avoid writing $P$ to HBM and directly use it with $V$ loaded from HBM to computer $O$.
But the authors also say that GPUs have a massive number of threads to execute an operation (called a kernel). Each kernel loads inputs from HBM to registers and SRAM, computes, then writes outputs to HBM. So it is because the computation of attention is divided into multiple kernels, e.g., $P=softmax(S)$, so these individual kernels should read data from HBM, and write the result back to HBM for the second kernel to read.
Solution?
Obviously, we can fuse these kernels into one kernel to be executed in SRAM without reading $S$ from and writing $P$ to HBM. This is actually what FlashAttention is doing.
FlashAttention via tiling and recomputation
Here is the algorithm for the forward implementation:

Basically, the tricks that divide $Q$ into $T_r$ segments along the rows, and divide $K$ and $V$ into $T_c$ segments along the columns is called tiling. So after tiling, the computation of attention layer is divided into $T_r\times T_c$ small pieces, for each piece the SRAM could locate all the intermediate results to finish the computation. We use $l\in \mathbb{R}^N$ to record the updated softmax normalization factor, and $m\in \mathbb{R}^N$ to record the maximum elements in rows. Because the the inner loop is long the columns of $K$, so $l$ and $m$ will only be finally determined after the whole inner loop.
The use of $m$, I guess, is to maintain the numerical stability to avoid huge numbers that can cause overflow.
If you still don’t understand the tiling, here is the original introduction:

where, we have to track $l$ and $m$ during tiling.
Actually, the above algorithm skips dropout, causal mask, and scaling of $QK^T$ by $1/\sqrt(d)$. But the addition of these operations is straightforward.
For backward implementation, it follows the similar spirit. One difference is that it additionally uses gradient checkpointing (activation recomputation) for the attention map, and the dropout mask can be also recomputed known the pseudo-random number generator in the forward pass. Please refer to the appendix in the original paper.
Complexity of communication (or HBM accesses)
Here, since FlashAttention prevent the movement of the data with size $N^2$, by combing all the movement from and to HBM, the communication complexity (number of HBM accesses) is proved to be $o(N2d2M^{-1})$.
Block-sparse FlashAttention
This is quite simple, since some techniques can be used to sparsify the attention maps block-wise to speed up inference, so we could safely skip all the spasified blocks out of the total $T_r\times T_c$ blocks.
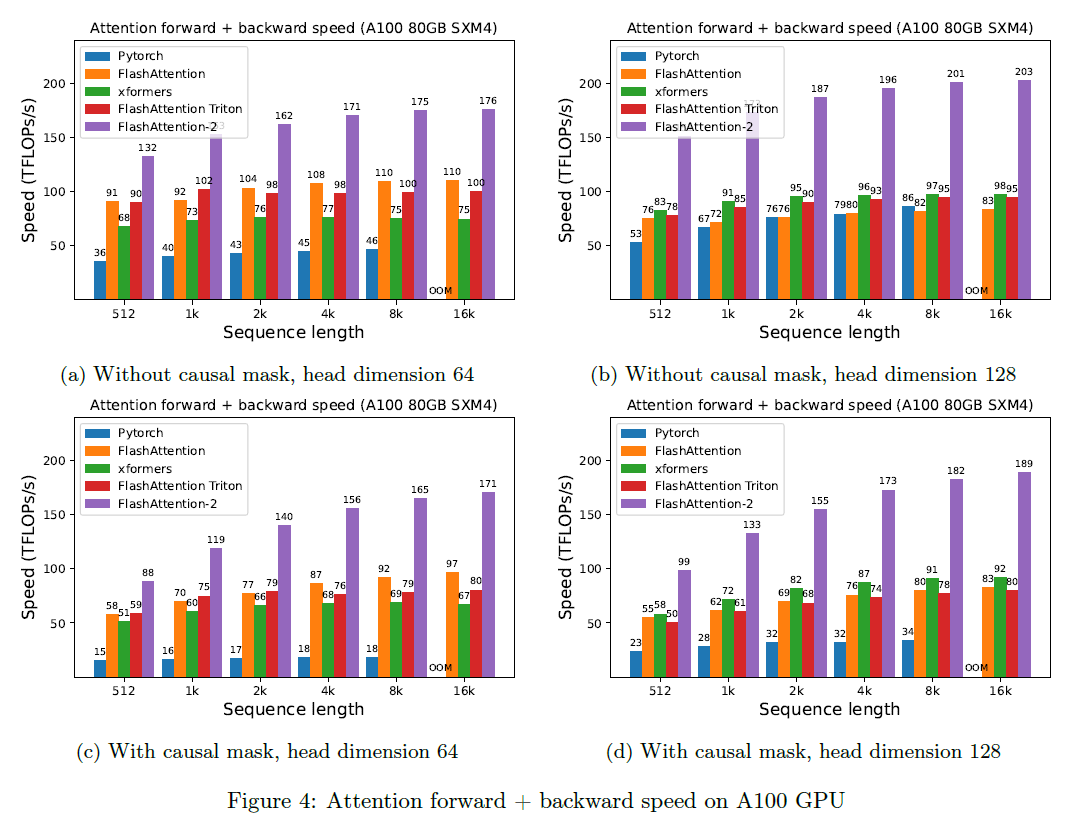
Results
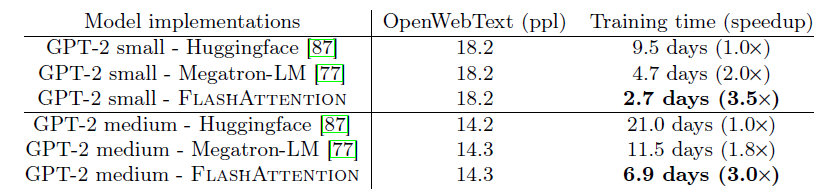
Above figure shows that for context length with 1K, FlashAttention gives higher speedup. And:

Conclusion:
IO is important, for memory-bound operations.
FlashAttention-2: Faster Attention with Better Parallelism and Work Partitioning
Background
The non-matmul FLOPs are now becoming a bottleneck since its throughput is $16\times$ slower than that of the matmul FLOPs. This is because matmul operations are highly optimized in GPUs.
So the solution is to reduce the number of non-matmul FLOPs in FlashAttention.
FlashAttention-2
Assuming $T_r=2$ and $T_c=2$, the tiling of computation can be expressed as:
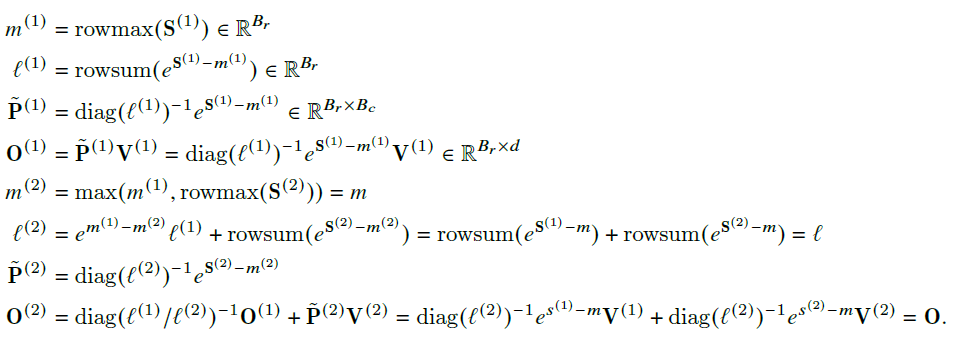
Then we found that

and (the below is for backpropagation)
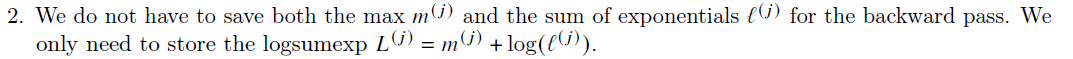
So the algorithm of forward propagation now becomes:

The algorithm for backward propagation follows the same spirit.
Another finding in the algorithm
We could see another big difference is that the order of loops is switched compared to original FlashAttention. Here, the outer loop is along the rows of $Q$, which means each iteration in the outer loop can be executed independently without communicating with each other. In other words, the outer loops can be executed in parallel. But the backward propagation should be further taken care of since it involves some communication between outer loop executions.
Parallelism
The original FlashAttention can be paralleled alongside data (or batch) and head. Based on the above finding, FlashAttention-2 can be further paralleled alongside its outer loop, i.e., the rows of $Q$, or the sequence.
For backward propagation, we also parallelize the computation along sequence but along the columns of $K$ and $V$, and use atomic adds to communicate between different workers.
The additional parallelism dimension allows us to better use of multiprocessors on the GPU to improve the occupancy of GPUs.
Results